Mapa del sitio

(M-9) Deducir los Senos y los Cosenos

Deducir el seno o el coseno de un ángulo arbitrario, necesita algo más de matemáticas que las tratadas aquí. Sin embargo, deducirlos de algunos ángulos especiales es relativamente directo. 

Ángulos Complementarios 

Primero observe que un triángulo rectángulo tiene dos ángulos. Como los tres ángulos (de cualquier triángulo) suman 180º, los dos ángulos agudos suman 90º. Por lo que resulta que si uno de los ángulos es de A grados, el otro (su "ángulo complementario") es de (90º-A). 

El seno y el coseno se definen con las siguientes relaciones: 

sen A = (lado opuesto a A)/(lado largo) 
cos A = (lado adyacente a A)/(lado largo)

Como el lado opuesto a A es el adyacente a (90°- A), resulta que el seno de un ángulo es el coseno del otro y viceversa: 

sen A = a/c = cos (90° - A) 
cos A = b/c = sen (90° - A)

Esto es de gran ayuda: deducir, por ejemplo, el seno y el coseno de 30º nos proporciona el seno y el coseno de 60°. 

(1) A = 45°

Si A = 45°, entonces también (90° - A) = 45°, y por consiguiente 
    sen 45° = cos 45°
Elevando al cuadrado 
    sen2 45° = cos2 45°
Sin embargo, anteriormente se halló que para cualquier ángulo A 
    sen2A + cos2A = 1
Por lo tanto 
    2 sen2 45° = 1 

    sen2 45° = 1/2

y si √ significa "raíz cuadrada de" 
    sen 45° = √(1/2)
Pulsando el botón de su calculadora obtiene 
    sen 45° = 0.707107... = cos 45°
Otra forma, algo más transparente, es escribir 
    sen2 45° = 1/2 = 2/4 

    sen 45° = √(2)/√(4) = √(2)/2

La raíz cuadrada de 2 es 1.4142135..., dividiéndola por dos se obtiene, como antes, 0.707107. 
 
 

(2) A = 30°, (90° - A) = 60°

Considere el triángulo PQR (dibujo) con los tres ángulos iguales a 60°. Por simetría, los tres lados son también iguales (existe una comprobación más rigurosa, pero la obviamos). Dibuje una línea QS perpendicular a PR: divide al triángulo original en dos triángulos rectángulos con los ángulos agudos de (30°, 60°), que son del tipo que nos interesa. Por simetría, los triángulos son de igual tamaño y forma ("congruentes") y por consiguiente, (obviando cualquier otra comprobación) 
 
    SR = (1/2) PR
En la notación del dibujo 
    a = (1/2) c 

    a/c = 1/2 = sen 30° = cos 60°

Continuando 
    sen2 30° = 1/4
Pero 
    sen2 30° + cos2 30° = 1
Así que 
    1/ 4 + cos2 30° = 1
Restando 1/4 de ambos lados 
    cos2 30° = 3/4 

    cos 30° = √(3)/ √(4) = √(3)/2  =  1.7320508/2 

    cos 30° = 0.8660254 = sen 60°

(3) A = 90° , (90° - A) = 0

Será bastante más difícil dibujar un triángulo rectángulo con un segundo ángulo también de 90º, debido a que el tercer ángulo deberá ser de 0º. Pero podemos visualizar este extraño triángulo como un caso límite de triángulos finos con un ángulo A que es muy pronunciado y su complementario (90° - A) muy pequeño (dibujo). En el caso límite 
 
 

cos A = b/c = 0

y como 

1 = sen2A + cos2A = sen2A + 0

resulta que 

sen2A = 1     sen A = 1

Por consiguiente 

cos 90° = sen 0° = 0 
sen 90° = cos 0° = 1

En la tabla completa se lee
 

A 0° 30°  45° 60° 90°
sen A 0 0.5 0.707107 0.866025 1
cos A 1 0.866025 0.707107 0.5 0

Podrá dibujar una buena gráfica de los senA y cosA usando los puntos anteriores 

(4) Postgraduado: A = 15°, (90° - A) = 75°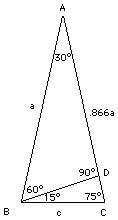

Las deducciones y tabla anteriores un procedimiento estándar en cualquier curso o texto de trigonometría. Sin embargo observará los huecos entre  0° y 30°, y entre 60° y 90°. Si queremos que el ángulo A se incremente en pasos iguales de 15o, necesitaremos los senos y cosenos de 15° y 75°. 

¿Está interesado? Aquí está lo que deberemos hacer; ¡tome su calculadora! 

Dibuje un triángulo ABC, con un ángulo A igual a 30° y los dos ángulos de la base igual a 75° ambos. Luego dibuje la línea  BD perpendicular a AC (vea el dibujo de la derecha). Por simetría, los lados AB y AC tienen la misma longitud; denomine la longitud por la letra a. 

El triángulo ABD tiene ángulos de 90, 60 y 30 grados, y es del tipo examinado anteriormente. Obtenemos 

BD = a sen 30° = 0.5 a
AD = a cos 30° = 0.866025 a

Luego 

DC = AC - AD = a - 0.866025 a = 0.133975 a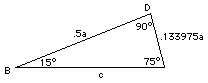

Ahora mire el triángulo BDC: sus ángulos mayores son iguales a  90° y 75°, obligando al ángulo restante a ser igual a 15°. Usando el  teorema de Pitágoras, si denominamos c al lado más largo, obtenemos 

BD2 + CD2 = c2 = (0.5 a)2 + (0.133975 a)2
= 0.25 a2 + 0.0179493 a2 = 0.2679493 a2

Extrayendo la raiz cuadrada 

c = 0.517638 a

Por esto, a 5 decimales (e implicando igualmente al ángulo complementario de 75° ) 

sen 15° = 0.133975/0.517638 = 0.25882 = cos 75° 
cos 15° = 0.500000/0.517638 = 0.96593 = sen 75°

Ahora vaya y dibuje su gráfica.

Página principal en Español (índice)


Índice Matemático              Linea del Tiempo              Glosario .

Próxima Etapa:  #M-10   Pasar de 90 Grados

Author and Curator:   Dr. David P. Stern
     Messages to Dr.Stern:   stargaze("at" symbol)phy6.org   (English, please) .

Spanish translation by J. Méndez

Last updated 13 December 2001